Solution for #110 is the score for the first roll. Solution for #2The only lockers that remain open are perfect squares (1, 4, 9, 16, etc) because they are the only numbers divisible by an odd number of whole numbers; every factor other than the number's square root is paired up with another. Thus, these lockers will be "changed" an odd number of times, which means they will be left open. All the other numbers are divisible by an even number of factors and will consequently end up closed. So the number of open lockers is the number of perfect squares less than or equal to one thousand. These numbers are one squared, two squared, three squared, four squared, and so on, up to thirty one squared. (Thirty two squared is greater than one thousand, and therefore out of range.) So the answer is thirty one. Solution for #3Use the first two cuts to cut an 'X' in the top of the cake. Now you have four pieces. Make the third cut horizontal, which will divide the four pieces into eight. Think of a two by two by two Rubik's cube. There's four pieces on the top tier and four more just underneath it. Solution for #4
Solution for #5
Solution for #6Not at all. He'll earn $5,368,709.12 on the thirtieth day alone. Solution for #7Let d be the distance to the store, T be the time it gets to get there, t be the time it takes to get back, and A be the average speed (which is what we want to find out). As we know from elementary mathematics, distance equals rate times time: d = 20T Now that we have expressions for T and t, we can come up with an equation that describes the round trip: 2d = A(T + t) So the average speed is 24 mph. If this seems strange to you, consider that more time is spent traveling at 20 mph than time spent at 30 mph, so the "20 mph" figure should count more toward the average. Solution for #8Let d be the distance to the store, T be the time it gets to get there, t be the time it takes to get back, and R be the speed you travel on the return trip (which is what we want to find out). As we know from elementary mathematics, distance equals rate times time: d = 20T Now that we have expressions for T and t, we can come up with an equation that describes the round trip: 2d = 40(T + t) Here we have worked our way into a paradox. The reason, simply, is that you have to travel back at an infinite speed to make your average speed 40 mph. This may seem strange, but consider that, the faster your return trip, the quicker you make it, and consequently, this faster speed has a lesser impact on the average speed. If you traveled the return trip instantaneously, this would be equivalent to traveling double the distance in the same amount of time as the one-way trip. So if the rate of speed of the return trip is infinite, you do indeed get an average speed of 40 mph. Solution for #9There is only one solution, discounting mirror image solutions and rotations:
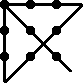
Solution for #10Since the trains are 100 miles apart, and the trains are traveling toward each other at 40 and 60 mph, the trains will collide in one hour. The bird will have been flying for an hour at 90 miles per hour at that point, so the bird will have traveled 90 miles. Solution for #11The problem is with the division that takes place between the fourth and fifth equations. Since a = b, a - b is zero, and you can't divide by zero. Solution for #12Actually there's nothing wrong with it. Ten does equal 9.99999..., as this proof clearly shows. Solution for #13If the product of his three children's ages is 72, there are the following possibilities: 1 * 1 * 72 = 72 Isaac later gives Albert the sum of their ages, but we don't know what number he says. We do, however, know that Albert can't figure it out from that information. So, we take the possibilities listed above and add them up: 1 + 1 + 72 = 74 The only way Albert wouldn't be able to figure out Isaac children's ages by knowing the sum is if the sum was 14, because there are two possibilities. So either the children's ages are 2, 6, and 6, or 3, 3, and 8. But Isaac points out that he has a youngest child. So the ages must be 2, 6, and 6. Solution for #14The hour hand is exactly on a minute mark five times per hour -- on the hour, twelve minutes past the hour, twenty four minutes past, thirty six minutes past, and forty eight minutes past. Let X be the number of hours, and Y be the number of minutes past the hour. When the hour hand is on a minute mark, the position of the hour hand is 5X + Y/12, and the position of the minute hand is Y. On the first occasion, Y = 5X + Y/12 + 6. This is equivalent to 60X = 11Y - 72. Since Y can only take one of the values in the set { 0, 12, 24, 36, 48 }, it can be determined that the only legal values for the equation are X = 1 and Y = 12. So the time is 1:12. Similarly, the second occasion's equation is 60X = 11Y - 84. The only legal values here are X = 3 and Y = 24. So the time is 3:24. Between 1:12 and 3:24, two hours and twelve minutes have elapsed. Solution for #15Let c be the number of chickens, and r be the number of rabbits. r + c = 72 To solve the equations, we multiply the first by two, then subtract the second. 2r + 2c = 144 So there are 44 chickens and 28 rabbits in the cage. Solution for #16Let g be the total units of grass in the field before the sheep are turned out. Let s be the number of units of grass each sheep eats per day. We must determine the constant values of g and r from the information given in the problem. The total number of grass units eaten equals the number of days times the amount of grass the sheep eat per day. From this, we can construct two equations: g + 20r = 20(10s) Reducing the equations, we obtain: g + 20r = 200s Subtract one equation from the other: 10r = 50s So r equals 5s. Substituting back, we discover g equals 100s. Now we construct an equation for the case of having 25 sheep turned out in the field, where x is the number of days it takes the sheep to eat all the grass: g + xr = x(25s) So 25 sheep would consume all the grass in the field in 5 days. Solution for #17Let a be the number of red squeegies you buy. Let b be the number of yellow squeegies you buy. Let c be the number of blue squeegies you buy. We know two equations: a + b + c = 100 By multiplying the first equation by 6 and then 3, then subtracting these two equations from the second, we can come up with two more equations: 6a + 6b + 6c = 600 Normally, two equations isn't enough to solve for three variables. But we know that a and b are nonnegative integers. So, if 3b ≥ 0, then 500 - 5.9c ≥ 0. This means c ≤ 84.75. Also, if 3a ≥ 0, then 2.9c - 200 > 0. This means c ≥ 68.97. However, since buying blue squeegies is the only way to spend a fraction of a dollar, the number of blue squeegies we buy must cost an even dollar amount. The only two numbers of blue squeegies we can buy between 68.97 and 84.75 that satisfy this condition are 70 and 80. If we substitute 80 for c in the last two equations listed above, we can solve for a, which equals 10.67, and b, which equals 9.33. But the values of a and b must be integers, so we know this is not the solution. If we substitute 70 for c in the last two equations listed above, we can solve for a, which equals 1, and b, which equals 29. So one red squeegie must be bought for $6.00, 29 yellow squeegies must be bought for $87.00, and 70 blue squeegies must be bought for $7.00. Solution for #18Alternate Solution #1 Let x be the age of the man at the time of his death. His age consists of the number of years he spent as a child plus the number of years he spent as a teenager plus the number of years between his coming of age and his marriage plus five plus his son's age (half his own) plus four. In mathematical terms, this is: x = x/6 + x/12 + x/7 + 5 + x/2 + 4 So the man lived to be 84 years old. Alternate Solution #2 The man lived 1/12 of his life as a teenager. There are seven teen years. 7 × 12 = 84. Solution for #19Alternate Solution #1 Let s be the total distance of the journey to the hotel. Let v be walking speed. So 2v is the bike's speed, and 8v is the train's speed. Let I be the time it took for Isaac to complete the journey, and A be the time it took for Albert to complete the journey. Since distance equals rate times time, we have two equations, one for I and one for A: I = (s/2)/8v + (s/2)/v = s/16v + s/2v Note that I exceeds A by s/16v. Albert will reach the hotel first. Alternate Solution #2 The problem may be solved more easily with simple logic. If the bicycle is twice as fast as walking, the time it takes to bike the whole way is equal to the time it takes to walk half the way. So if the train's speed is anything shy of infinite, biking will still be faster. Solution for #20You can buy any number of nuggets that is evenly divisible by three except for three just by using combinations of boxes of 6 and boxes of 9. (Use at most one box of 9, then multiples of boxes of 6.) If the number is not divisible by three, use a box of 20. If, after a box of 20 is purchased, the remaining number is divisible by three, you're all set. Otherwise, use a second box of 20. The remaining number will necessarily be divisible by 3, and you're all set. So the largest number that cannot be purchased would be one that requires two boxes of 20 before the remainder is reduced to a number divisible by three. Since three is the only number evenly divisible by three that cannot be purchased, the largest impossible number is 3 + 20 + 20 = 43. Solution for #21Let x equal the number of marbles in a small bag, and y represent the number of marbles in a large bag. We know that the following equation holds: 7x + 18y = 233 Ordinarily, it is not possible to solve for two unknowns with a single equation; however, we also know that x and y are positive integers and that x is less than y. We can narrow the search by solving for the highest and lowest possible values for y: Assume y = x: Since y must be an integer, y ≥ 10. Assume y = 1: Since y must be an integer, y ≤ 12. So the only possible values for y are 10, 11, and 12. Substituting each of these values into the original equation, we can find the corresponding values of x. Respectively, they are 7.57, 5, and 2.42. Since x must be an integer, the correct solution is x = 5 and y = 11. So the small bags of marbles contained five each, and the large bags contained eleven each. Solution for #22For starters, the answer is not 1/2. When the coin is drawn, there are four possibilities, each of which is equally likely:
The problem tells us that the last possibility did not occur. Therefore, there are three remaining possibilities, each of which is equally likely. Of the three, two of the possibilities will show heads on the other side; only one will show tails on the other side. So the probability that the other side of the coin is heads is two thirds. Solution for #23It should only take nine minutes to cook the egg. If you want to try to figure out how it is done in this short amount of time before seeing the answer, stop reading now. To start, flip both hourglasses over and put the egg in the water. When the four minute hourglass runs out, flip it back over immediately. When the seven minute hourglass runs out, flip that back over immediately too. One minute later, the four minute hourglass will run out again. At this point, flip the seven minute hourglass back over. The seven minute hourglass had only been running for a minute, so when it is flipped over again it will only run for a minute more before running out. When it does, exactly nine minutes will have passed, and the egg is done. Solution for #24First figure out how much three of each time of stamp costs (63 cents). Now you need to figure out which two stamps to get a fourth of that will make the total cost some number of cents divisible by ten. You can't get enough to make 80 cents with two stamps, so the total cost must be 70 cents and the cost of the two extra stamps must be 7 cents. So the two extra stamps are a two-cent stamp and a five-cent stamp. Solution for #25Let's break the question down into steps. We know that a boy and a half can eat a hot dog and a half in a minute and a half. So how many hot dogs could six boys eat in a minute and a half? We have the same amount of time, but four times as many boys, so the answer is four times as many hot dogs -- six, to be precise. But now let's consider what six boys could eat in six minutes. We now have four times as much time, so the answer is four times as many hot dogs -- specifically, 24. Solution for #26The original number of coins must be a number such that you can subtract one and multiply by four fifths and get an integer. These numbers are 6, 11, 16, 21, 26, and so on. But the pile remaining after the first pirate has taken his gold must also have this property. So the possibilities for the original number are 16, 36, 56, 76, 96, and so on. The pile remaining after the second pirate has taken his gold must also have this property. So the possibilities for the original number are 76, 156, 236, 316, 396, and so on. The pile remaining after the third pirate has taken his gold must also have this property. So the possibilities for the original number are 316, 636, 956, 1276, 1596, and so on. The pile remaining after the fourth pirate has taken his gold must also have this property. The smallest possibility for this is 1276. This number is the number of gold pieces in the chest the fourth pirate left behind (for the fifth pirate to divide). The fourth pirate hid a quarter of this number, plus one extra, just before the fifth pirate got there. So the third pirate left behind 1276 + 1276/4 + 1 = 1596 gold pieces. The third pirate hid a quarter of this number, plus one extra, just before the fourth pirate got there. So the second pirate left behind 1596 + 1596/4 + 1 = 1996 gold pieces. The second pirate hid a quarter of this number, plus one extra, just before the third pirate got there. So the first pirate left behind 1996 + 1996/4 + 1 = 2496 gold pieces. The first pirate hid a quarter of this number, plus one extra. So the original number of coins must have been 2496 + 2496/4 + 1 = 3121 gold pieces. Solution for #2750 factorial includes, as factors, 10, 20, 30, 40, and 50. Therefore, the value of 50 factorial must end in at least five zeroes. The number given only ends in three zeroes. The correct value of 50 factorial is close to this, however. It's 30414093201713378043612608166064768844377641568960512000000000000. Solution for #284 and 12. Solution for #29A half dollar, a quarter, and four dimes. Solution for #30After ten sales of five apples, all the three-for-fifty-cents apples are sold; the remainder is still sold at five for a dollar when they should be sold at two for fifty cents. Solution for #31No. Six dozen dozen dozen is 6 × 12 × 12 × 12. A half dozen dozen dozen is just 6 × 12 × 12. Solution for #32Alligator breeder #1 had 49 alligators, and alligator breeder #2 had 35. Solution for #3399 99/99 Solution for #34Let S be the number of sheep and C be the number of chickens. So: 2S = C We can rephrase the first equation thusly: 6S - 3C = 0 And then we can add this to the second equation, which yields: 11S = 99 By solving for S, we find that S equals 9. By substituting back in one of the original equations, we find that C equals 18. So there are nine sheep and eighteen chickens. Solution for #35The circumference of a circle is 2πr, where r is the radius of the circle. If you want a rope that is one yard above the ground, this radius is larger by one yard. Let R be this new radius. So R = r + 1. Let x be the amount of extra rope required by the eccentric's rival. So: x = (2π(r + 1)) - (2πr) So x is about 6.2832 yards. Note that this answer does not depend on the radius of the circle. If the eccentric and his rival were attempting to tie up a baseball rather than the earth, the amount of additional required rope would be the same amount. Solution for #36The head and tail are each three inches long; the rest is nine. Solution for #37Alternate Solution #1 A half dollar, 39 dimes, and 60 pennies. Alternate Solution #2 A dollar coin, a half dollar, 28 dimes, and 70 pennies. Alternate Solution #3 Two dollar coins, a half dollar, 17 dimes, and 80 pennies. Solution for #3862.5 chocolates. Solution for #39If 100 pounds of potatoes is 1% potato matter, then that means there is one pound of potato matter. After the potatoes dehydrated somewhat, this one pound accounted for 2% of the total mass (with the remaining 98% being water). One pound is 2% of 50 pounds, so the total mass of the potatoes after sitting out in the sun is 50 pounds. Solution for #40Let b be the number of birds, and c be the number of cages. The problem gives us two equations, which we can merge together to solve for c: b = c + 1 Now we substitute 3 for c in one of the original equations to discover that b equals 4. So there are four canaries and three cages. Solution for #41Let c be the number of cows purchased, p be the number of pigs purchased, and s be the number of sheep purchased. We know that the total number of animals purchased is 100. Moreover, we know that the total cost of each one adds up to $100. This gives us two equations: c + p + s = 100 If we multiply the second equation by two, that gives us: 20c + 6p + s = 200 If we take this equation and subtract the first equation, we eliminate s entirely and wind up with: 19c + 5p = 100 We can rewrite this equation like so: 100 - 19c = 5p Since c and p are constrained to positive integers, we can narrow down the possible solutions pretty quickly. We know that c cannot be 6 or higher, because then p would have to be negative for the equation to hold. So we only need to consider 1, 2, 3, 4, and 5 as possible values for c. Substituting 1, 2, 3, or 4 for c, however, results in the left-hand side of the equation being unevenly divisible by 5, which means p would have to be a non-integer for the equation to hold. So c must be 5. Substituting c allows us to solve for p: 100 - 19c = 5p Now we can substitute the values for c and p in one of the two original equations (the first is easiest) and solve for s: c + p + s = 100 The farmer purchased five cows ($50), one pig ($3), and 94 sheep ($47). |
|